In material- und produktionswirtschaftlichen Aus- und Fortbildungen beschränken sich viele Dozenten, und noch mehr Rahmenstoffpläne, auf die Bestellmengen- und Losgrößenrechnung nach Andler. Das ist die berühmte Formel mit der Quadratwurzel, die eine optimale Bestellmenge Mopt zustande bringt. Wegen der großen Häufigkeit der Methode, bieten wir auch im öffentlichen Bereich mehrere Excel-Rechner dazu an (grundlegendes Modell, Rechner mit Lagrange-Multiplikator). Der Haken an der Sache: kaum jemand kann das in der betrieblichen Realität verwenden, weil ein Jahresbedarf gegeben sein muß. Wer aber kennt den Materialbedarf für ein Jahr im voraus?
Dabei gibt es Methoden, die viel besser und damit viel praxisrelevanter sind, die aber kaum jemand kennt, weil die Dozenten sie nicht kennen. Bestes Beispiel hierfür ist die Bestellmengen- oder Losgrößenrechnung nach Groff, die eine Erweiterung der andler'schen Methode ist. Die Methode setzt aber keinen bekannten Jahresbedarf voraus, sondern nur die jeweils nächsten Bedarfstermine. Das macht das Verfahren wesentlich realitätsnäher. Ein wenig kostenrechnerische Grundlagen sind freilich auch hier vonnöten.
Die wesentliche Verbesserung bei der Groff-Methode ist, daß die Notwendigkeit entfällt, einen Jahresbedarf zu kennen. Hierfür wird die traditionelle Lagerkostenformel auf die wirkliche (und nicht die gesamte) Lagerdauer bezogen. Auf diese Weise wird es möglich, nur die bekannten, in naher Zukunft liegenden Bedarfstermine zu berechnen. Die Zeit, für die eine Planung möglich ist, heißt dabei Horizont. Die Andler-Methode berechnet eine – meist wenig realistische, weil krumme – Bestellmenge. Das Groff-Verfahren hingegen rechnet so viele Bedarfstermine ab dem nächsten Bedarfsfall in die Zukunft hinein zusammen, daß eine mindestens angenäherte Kostenminimierung entsteht.
Hierzu muß die traditionelle Lagerkostenformel verändert werden. Traditionell berechnet man die Lagerkosten KL aus der mittleren Kapitalbindung, dem Wert q eines Exemplares und dem Material-Gemeinkostenzuschlag MGZ auf folgende Weise:
![]()
Die Groff-Methode bezieht hier aber die wirkliche Lagerdauer LDreal als Teil des Jahres (mit realistisch 365 Tagen) ein. Es entsteht damit:
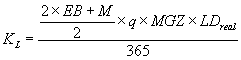
Diese Formel besagt, welche Lagerkosten für eine bestimmte, in Tagen bekannte Lagerdauer bestehen. Für jeden Bedarfstermin können damit eigenständig die Lagerkosten für die wirkliche (und nicht eine statistische) Lagerdauer berechnet werden.
Betrachten wir ein Beispiel: ein Unternehmen benötigt ein Halbfabrikat, dessen Wert q = 70 Euro/Stück beträgt. Ein Eiserner Bestand soll nicht geführt werden. Ein Bestellvorgang verursache Kosten i.H.v. 200 Euro. Der Materialgemeinkostenzuschlag betrage 10%. Zu den links genannten bekannten Bedarfsterminen bestehen die genannten Bedarfsmengen:
| Bedarfstermin | Bedarfsmenge | Lagerkosten | Bestellkosten | Kostensumme | Kostendifferenz | ||
| pro Periode | kumuliert | pro Periode | kumuliert | ||||
| 12.05.2009 | 1.000 Stück | 0,00 € | 0,00 € | 200,00 € | 1.600,00 € | 1.600,00 € | –200,00 € |
| 15.05.2009 | 2.000 Stück | 57,53 € | 57,53 € | 400,00 € | 1.400,00 € | 1.457,53 € | –342,47 € |
| 20.05.2009 | 1.500 Stück | 115,07 € | 172,60 € | 600,00 € | 1.200,00 € | 1.372,60 € | –427,40 € |
| 29.05.2009 | 3.000 Stück | 489,04 € | 661,64 € | 800,00 € | 1.000,00 € | 1.661,64 € | –138,36 € |
| 03.06.2009 | 500 Stück | 105,48 € | 767,12 € | 1.000,00 € | 800,00 € | 1.567,12 € | –232,88 € |
| 12.06.2009 | 1.200 Stück | 356,71 € | 1.123,84 € | 1.200,00 € | 600,00 € | 1.723,84 € | –76,16 € |
| 23.06.2009 | 2.000 Stück | 805,48 € | 1.929,32 € | 1.400,00 € | 400,00 € | 2.329,32 € | 529,32 € |
| 03.07.2009 | 1.500 Stück | 747,95 € | 2.677,26 € | 1.600,00 € | 200,00 € | 2.877,26 € | 1.077,26 € |
Da heute der 12. Mai ist, muß die für heute benötigte Menge nicht mehr gelagert werden. Die Lagerkosten nur für heute sind also stets null. Der 15. Mai liegt aber drei Tage in der Zukunft. Soll der Durchschnitt aus null und 2.000 Stück x 70 Euro zu 10% Gemeinkostenzuschlag für drei Tage gelagert werden, so entstehen Kosten i.H.v. 57,53 Euro. Der nächste Bedarfstermin ist der 20. Mai. Der liegt acht Tage in der Zukunft. Den Durchschnitt aus EB = 0 und M = 1.500 Stück, bewertet zu je Exemplar 70 Euro, verursacht Lagerkosten i.H.v. 115,07 Euro. Undsoweiter.
Da die heute benötigten 1.000 Stück bestellt werden müssen, sind Bestellkosten i.H.v. 200 Euro zu verrechnen. Das ist in der Bestellkosten-Spalte ausgewiesen. Da für heute ja keine Lagerkosten entstehen, ist der Kostensaldo aus KL – KB in der rechten Spalte negativ.
Werden die ersten zwei Bedarfsmengen (im Abstand von drei Tagen) separat bestellt, so beträgt der Kostensaldo aber für diese zwei Bestellungen zusammen 57,53 Euro – 400 Euro (für zwei Bestellungen!) = –342,47 Euro. Diese negative Zahl besagt, daß es um 342,47 Euro günstiger ist, die ersten beiden Bestellungen zu einer Sammelbestellung zusammenzufassen, also zu lagern anstatt zwei Mal die Bestellkosten zu verrechnen.
Will man die ersten drei Bestellungen zusammenfassen, so betragen die (kumulierten) Lagerkosten 0 Euro + 57,53 Euro + 115,07 Euro = 172,60 Euro. Drei Bestellungen kosten aber 600 Euro. Der Saldo beträgt also –427,40 Euro. Auch die ersten drei Bedarfsmengen sollten also zu einer Gesamtbestellung zusammengefaßt werden.
Erst der Nulldurchgang in der Saldenspalte rechte zeigt die Anzahl der zusammenzufassenden Bestellungen an. Im Beispiel ist erst für den 23.06.2009 erstmals eine positive Zahl zu sehen. Das bedeutet, daß die ersten sechs Bedarfstermine vom 12.05.2009 bis zum 12.06.2009 mit insgesamt 9.200 Stück zusammenzufassen, also in einer einzigen Sammelbestellung zu ordern und dann bis zum jeweiligen Bedarfstermin zu lagern sind. Dies ist die optimale, und zugleich auch gleich beste praktisch mögliche, Bestellmenge.
Dieses Verfahren ist eigentlich eine Weiterentwicklung der Andler-Methode. Das wird augenfällig, wenn man den Kostenverlauf und die Kostendifferenz mit dem über das Bestellverhalten entscheidenden Nulldurchgang in einer Grafik visualisiert:
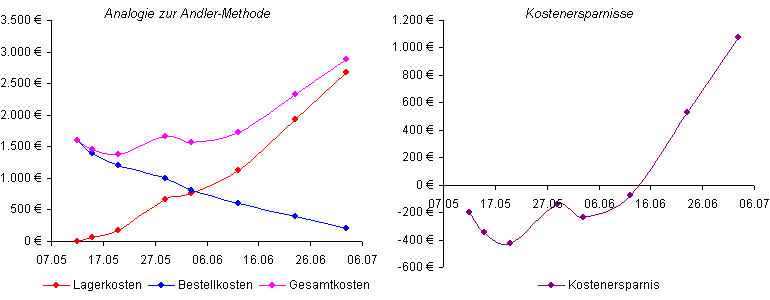
Die Kostenverläufe sind hierbei aber "unregelmäßig", weil die Bedarfsmengen und deren Zeitabstände nicht regelmäßig sind. Das führt zu dem ungleichmäßigen Kostenverlauf. Das erklärt auch, warum es hier (anders als bei Andler) eben nicht auf ein minimum der Kostensummenspalte, sondern auf den Nulldurchgang ankommt: Die Kostensummenspalte setzt die von unten nach oben aufsteigende Kumulation der Bestellkosten voraus, und ist daher nicht vom Bestellverhalten, sondern auch vom Horizont abhänguig. Nur die Kostendifferenzspalte ganz rechts aus kumulierten Lagerkosten minus vorwärts kumulierten Bestellkosten ist insofern aussagekräftig.
Ein besonderer Vorteil dieser Methode ist ihre Flexibilität. Legt man nämlich die oben demonstrierte Formel für die Lagerkosten zugrunde, so impliziert das im Anschluß an Andler, daß ein Durchschnitt aus der Bestellmenge M und dem Eisernen Bestand EBgelagert wird. Im Einkauf würde dies bedeuten, daß das Lager sogleich nach einem Lagerzugang langsam bis zum Bedarfstermin abgebaut wird. Das ist u.U. wenig realistisch, aber leicht anzupassen.
Nimmt man einen schlagartigen Lagerzugang der zusammengefaßten Bestellungen heute, und einen ebenfalls schlagartigen Lagerabgang der ganzen Bedarfsmenge am Bedarfstermin an, wie es etwa im Handel realistischer wäre, so muß man nur die Durchschnittskomponente aus der Lagerkostenformel entfernen:
![]()
Natürlich ist der durchschnittliche Kapitalbindungswert im Lager jetzt größer. Damit ändert sich auch die Tabelle. Nunmehr sind, wie der Nulldurchgang zeigt, aufgrund derselben Ausgangsdaten (!), also nur durch die Änderung der Annahme über den Lagerabgang, nur noch die ersten drei Bestellmengen zu einer Sammelbestellung i.H.v. 4.500 Stück zusammenzufassen:
| Bedarfstermin | Bedarfsmenge | Lagerkosten | Bestellkosten | Kostensumme | Kostendifferenz | ||
| pro Periode | kumuliert | pro Periode | kumuliert | ||||
| 12.05.2009 | 1.000 Stück | 0,00 € | 0,00 € | 200,00 € | 1.600,00 € | 1.600,00 € | –200,00 € |
| 15.05.2009 | 2.000 Stück | 115,07 € | 115,07 € | 400,00 € | 1.400,00 € | 1.515,07 € | –284,93 € |
| 20.05.2009 | 1.500 Stück | 230,14 € | 345,21 € | 600,00 € | 1.200,00 € | 1.545,21 € | –254,79 € |
| 29.05.2009 | 3.000 Stück | 978,08 € | 1.323,29 € | 800,00 € | 1.000,00 € | 2.323,29 € | 523,29 € |
| 03.06.2009 | 500 Stück | 210,96 € | 1.534,25 € | 1.000,00 € | 800,00 € | 2.334,25 € | 534,25 € |
| 12.06.2009 | 1.200 Stück | 713,42 € | 2.247,67 € | 1.200,00 € | 600,00 € | 2.847,67 € | 1.047,67 € |
| 23.06.2009 | 2.000 Stück | 1.610,96 € | 3.858,63 € | 1.400,00 € | 400,00 € | 4.258,63 € | 2.458,63 € |
| 03.07.2009 | 1.500 Stück | 1.495,89 € | 5.354,52 € | 1.600,00 € | 200,00 € | 5.554,52 € | 3.754,52 € |
Das macht die Sache außerordentlich praxistauglich, denn mit ein wenig Programmieraufwand können auch ganz unregelmäßige Entnahmemuster, die z.B. aus dem Netzplan und dem Maschinenbelegungsplan der Produktionsabteilung resultieren, recht präzise berechnet werden. Die Groff-Methode ist damit weitaus anpassungsfähiger als das alte Andler-Verfahren. ich empfehle daher meinen Beratungspartnern fast immer die Groff-Methode. Daß sowas in den üblichen Aus- und Fortbildungen meist fehlt, ist ein großer Mangel.
Die Groff-Methode ist übrigens nicht die einzige Alternative zum angejahrten Andler-Verfahren. Schon vor knapp sechs Jahren berichteten wir an dieser Stelle über den Wagner-Whitin-Algorithmus. Der Leser mag selbst beurteilen, welche Methode für sein individuelles Lager- und Bestelloptimierungsproblem besser paßt. Hilfe hierzu ist ggfs. auch vom BWL-Boten zu erwarten, aber nur imForum für Betriebswirtschaft kostenlos 🙂
Links zum Thema: Grundlegende Lagerkennziffernrechnung für Excel® | Lagerkennziffernrechnung mit Lagrange-Multiplikator für Excel® | Losgrößen- und Bestellmengenplanung nach Wagner/Whitin | Formelsammlung der BWL | Forum für Betriebswirtschaft(interne Links)







