Die Break Even Rechnung ist immer wieder für eine ordentliche Überraschung gut, und in einer Prüfung Technischer Betriebswirt liegt mir eine echte Knallschote vor, die sich die Kämmerlinge da ausgedacht haben. Wir präsentieren an dieser Stelle die dahintersteckende etwas verquere Denkweise und Lösungsstrategie zum Nutzen aller, die auch die offiziell angegebene Lösung vorliegen haben aber dennoch nicht verstehen. Der Beitrag ergänzt einen früheren Beitrag zur Break Even Prüfungsstrategie und zeigt erneut, daß dies ein besonders wichtiges (und auch besonders gefährliches) Prüfungsthema ist.
| Produkte | 1 | 2 | 3 |
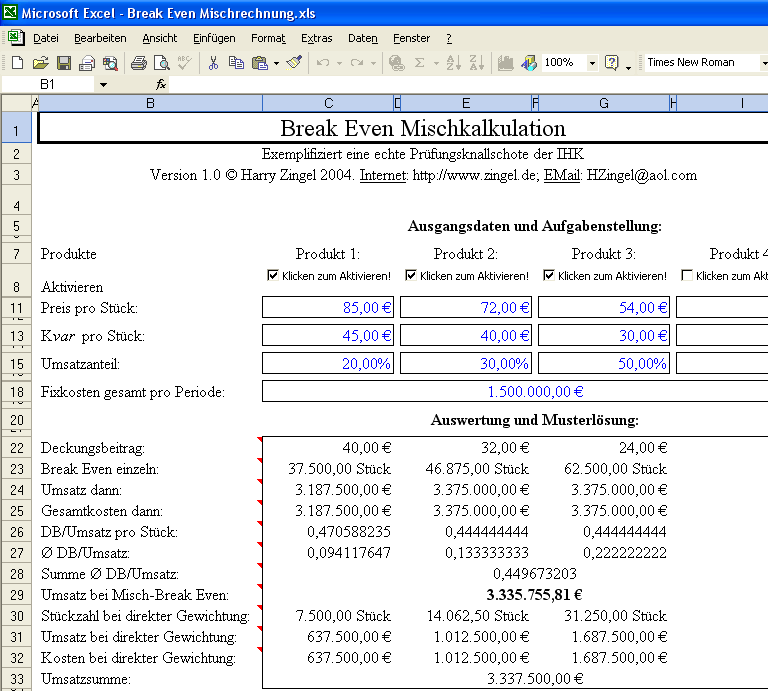
| Preis/Stück | 85 EUR | 72 EUR | 54 EUR |
| Kvar/Stück | 45 EUR | 40 EUR | 30 EUR |
| Umsatzverhältnis | 20% | 30% | 50% |
Ein Unternehmen produziert drei Produkte (1, 2 und 3), für die die nebenstehenden Daten bekannt sind. Die geplanten Fixkosten betragen 1,5 Mio. EUR/Periode. Die Planpreise sind konstant (d.h., der Markt ist ein Polypol) und die Stückkosten sind ebenfalls unveränderlich. Das Mengenverhältnis ist vom Abnehmer bzw. vom Markt vorgegeben. Der Break Even Umsatz ist zu ermitteln. Weitere Daten sind aus der Aufgabe nicht zu ersehen. Wir holen also tief Luft und lesen uns erstmal die Zahlen durch…
Sobald wir uns von dem Schrecken erholt haben, überlegen wir, welches Werkzeug auf dies harte Nuß passen könnte. Die drei Deckungsbeiträge kann man auch als Gleichung zusammengassen, wobei X für die Anzahl der zu produzierenden und zu verkaufenden Exemplare steht: DB = 40 X1 + 32 X2 + 24 X3, oder das Ziel der Sache: 40 X1 + 32 X2 + 24 X3 = 1500000.
Es sind also drei Unbekannte vorhanden, aber kein Gleichungssystem (es ist ja nur eine Gleichung, um genau zu sein, eine Zielfunktion). Es gibt also viele Lösungen für das Problem, weil man das Ziel mit 37.500 X1 oder mit 46.875 X2 oder mit 62.500 X3 erreichen könnte. Die optimale Kombination von Produkten wird normalerweise durch relative DBs festgelegt (das wird mit einer einzigen Beschränkung in den Lehrgängen "Betriebswirt/IHK" und "Technischer Betriebswirt" ja ausgiebig durchexerziert). Sind es mehrere Restriktionen, so muß man das Simplex-Verfahren anwenden, aber das ist nicht in den IHK-Stoffplänen enthalten (und wird daher normalerweise nicht behandelt). Hier gibt es aber gar keine Beschränkung, so daß nur die %-Werte als Schlüssel zur Verteilung bleiben.
| Produkte | 1 | 2 | 3 |
| DBUF/Stück | 0,470588 | 0,444444 | 0,444444 |
| ØDBUF | 0,094118 | 0,133333 | 0,222222 |
Jetzt, da der Adrenalinspiegel deutlich steigt, bemerken wir, daß diese Aufgabe so gestrickt ist, daß kein Standard-Verfahren hilft. Der Auswendiglerner kriegt jetzt zitterige Hände und den ersten Schweißausbruch. Alles Pauken hat nichts geholfen – sicher von den Prüfungslyrikern beabsichtigt. Wir stellen aber fest, daß ja "nur" der Break Even Umsatz gefragt ist (und nicht die Menge!). Daher muß zunächst berechnet werden, wieviel % vom Umsatz DB entsteht ("DBUF/Stück") und wieviel das nach Gewichtung ist ("ØDBUF"). Das könnte ein Schlüssel in eine Lösung sein. Übrigens sind im offiziellen Lösungsvorschlag nur die nebenstehenden Zahlen ohne weitere Erläuterung angegeben, was bedeutet, daß selbst manche Prüfer mit der Lösung ihre lieben Probleme haben, denn was haben uns diese kryptischen Zahlen zu sagen?
Wir teilen nun die 1.500.000 EUR Planfixkosten durch die Summe der ØDBUF von 0,449673203 als Summe der letzten Spalte, und kriegen prompt 3.335.755,814 EUR raus, was der gemischte (!) DB-Umsatz ist. Hierzu muß man natürlich wissen Xmin = Kfix / DB oder Xmin = K<fix / (Pvk – Kvar). So einfach kann das gehen!
Zum Vergleich: wäre nur mit 37500 X1 der Xmin erzielt worden, wäre der Umsatz 3.187.500 EUR gewesen, bei 46.875 X2 wären es 3.375.000 EUR Umsatz gewesen und bei den oben schon festgestellten 62.500 X3 wären 3.375.000 EUR erlöst worden. Daß der berechnete Mischumsatz ganz in dieser Gegend liegt, bestätigt ganz offensichtlich unsere Lösung.
Nun, das ist die Lösung zu einer echten Kammerknallschote, die mir zwei besonders zielstrebige Lehrgangsteilnehmer vorhin freundlicherweise und etwas hilfesuchend mitgeteilt haben. Ich muß gestehen, daß ich auch erstmal dran geknackt habe, und die vorgegebene Musterlösung erschloß sich mir erst nach einigem Nachdenken. Und kein Mensch würde so in der Wirklichkeit denken. Aber im Vorfeld einer Prüfung ist das natürlich die falsche Frage.
Übrigens: der berechnete Umsatz setzt sich aus einer gebrochenen Zahl von herzustellenden Exemplaren zusammen, was kaum realistisch ist. Normalerweise hätte man es aber nämlich mindestens mit einer Ganzzahligkeitserfordernis, möglicherweise auch mit festen packungsgrößen, also einer Mengenrasterung zu tun, was das Problem weitaus komplexer machen würde. Aber das kommt sicher erst in der nächsten Prüfung dran…
Ach ja: Auf Anregung meiner beiden Teilnehmer (vielen Dank dafür) habe ich eine kleine Musterlösung programmiert.
>> Hier Musterlösung downloaden!
Links zum Thema: Break Even Rechnung: so versuchen die Prüfungslyriker Euch zu kippen! | Warum nicht alles, was Verlust erwirtschaftet, auch abgeschafft werden sollte | Skript zum Simplex-Verfahren | Break-Even Mischrechnung