Derzeit herrscht bekanntlich noch Ungewißheit darüber, die wie Prüfungen zum geprüften Betriebswirt nach neuer Verordnung inhaltlich aussehen werden, denn die erste Prüfung dieser Art wird erst in wenigen Tagen geschrieben. Wir haben, wie es sich für jeden guten Dozenten gehört, den neuen Rahmenstoffplan und natürlich die neuen IHK-Textbände eingehend studiert. Im Fach "Finanzwirtschaftliche Steuerung des Unternehmens" nimmt nunmehr die Kapitalbedarfsrechnung einen größeren Raum ein, und dabei werden auch mathematische Verfahren angewandt, die bisher für Kammerbetriebswirte tabu waren:
Die Kapitalbedarfsrechnung stellt dabei auf Bilanzpositionen ab, die umsatzabhängig, also veränderlich sind. Diese können auch mit den Mitteln der schließenden Statistik prognostozoert werden. Die nachfolgend dargestellte Methode halten wir für prüfungsgefährlich, weil sie – einschließlich der Formel und der Berechnung! – im Finanzwirtschafts-Textband auf S. 37 ff dargestellt wird. Es ist also imperativ für Dozenten, das hier zu inhalieren und zu vermitteln, und für Teilnehmer, sich damit vertieft auseinanderzusetzen:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Eine Unternehmung betrachtet die vier Bilanzen der vergangenen Jahre (nebenstehend). Das Anlagevermögen unterliegt einer linearen Wertminderung von 5 T€uro/Jahr. Das Eigenkapital ist konstant, weil keine Anteilseigner in die Unternehmung eingetreten sind oder die Gesellschaft verlassen haben und keine sonstigen Kapitalerhöhungen oder -Senkunden stattfanden oder geplant sind. Ebenfalls unveränderlich ist das langfristige Fremdkapital (ein endfälliges Darlehen).
Der Bestand an Waren sei umsatzabhängig. Er steigt, wenn der Umsatz steigt, und sinkt, wenn der Umsatz zurückgeht. In den vier betrachteten Jahren betrug der Umsatz 150, 160, 175 und 190 T€uro.
Der Kapitalbedarf des 5. Jahres ist unter der Maßgabe zu prognostizieren, daß das Eigenkapital und das langfristige Fremdkapital sich weiterhin nicht verändern und die Wertminderung des Anlagevermögens wie bisher fortgesetzt wird. Zudem seien alle Lager- und Verkaufsprozesse unverändert, d.h. der Zusammenhang zwischen Warenlager und Umsatz bleibe bestehen. Die Umsatzprognose für Jahr 5 betrage 220 T€uro und es werde in t = 5 mit einem Bestand an sonstigem Umlaufvermögen i.H.v. 25 T€uro gerechnet. Zudem soll eine aus den Daten zu begründende (!) Aussage über die Güte der gemachten Vorgersage gebildet werden. Arghh!
Dies unterscheidet sich arg von früheren "Laber-Fragen" in dieser Fortbildung. Der Wandel hin zu mehr numerisch-rationalen Inhalten ist kaum zu übersehen. Fangen wir mal mit der Kapitalbedarfsrechnung an. Hierzu ist erst der Warenbestand des 5. Jahres zu prognostizieren. Wenn es einen Zusammenhang zwischen Warenlager und Umsatz geben soll, was vereinfachend aber nachvollziehbar ist, dann liegt auf der Hand, daß dieser mit Hilfe der Regressionsrechnung berechnet werden kann. Der Zusammenhang ist also
Warenbestand = f(Umsatz)
|
Die lineare Regression kann man mit einem Computer schnell mal berechnen, aber Geräte mit Betriebssystem sind in der Kammerbetriebswirte-Prüfung nicht zugelassen. Man muß sich also per Taschenrechner die nebenstehende Hilfstabelle machen. Wir beachten, daß aus der zugrundeliegenden linearen KQ-Funktion Y* = A + B · X hervorgeht, daß X der Umsatz und Y der Warenbestand ist.
Sind diese Zahlen fertig, so rascheln wir in der hoffentlich mitgebrachten Formelsammlung nach der Regressionsformel und berechnen also A und B:
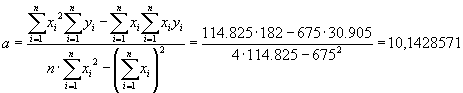 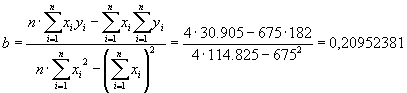 |
Die Regression erlaubt die Ableitung einer Gleichung aufgrund einzelner Meßwerte. Der Funktionstyp muß dabei zugrundegelegt werden, ist hier aber ausdrücklich als linear angenommen. Die Regressionslinie zeigt dann die höchste Wahrscheinlichkeit des Auftretens neuer Werte (Kleinste-Quadrate-Regression). Anders als in früheren Rahmenstoffplänen ist mit der neuen Verordnung sowas ausdrücklich relevant, wird im neuen Textband "Finanzwirtschaftliche Steuerung" aber nur mangelhaft erläutert. Der Dozent muß dieses Thema dennoch kennen und vermitteln!
Setzt man diese Ergebnisse in die lineare Ausgangsgleichung ein, so erhält man die folgende Warenbestandsprognose für t = 5:
![]()
Hieraus kann man eine Prognosebilanz für die Folgeperiode t = 5 ableiten. Das Anlagevermögen vermindert sich weiter um 5 durch Abschreibung und Eigenkapital und Darlehen bleiben konstant. Das führt zu folgendem Ergebnis:
| Prognosebilanz t = 5: | ||||||
| Aktiva | Passiva | |||||
| Anlagevermögen | 80,000 T€ | Eigenkapital | 80,000 T€ | |||
| Wareneinkauf | 56,238 T€ | lfr. Fremdkapital | 25,000 T€ | |||
| Sonstiges UV | 25,000 T€ | kfr. Fremdkapital | 56,238 T€ | |||
| 161,238 T€ | 161,238 T€ | |||||
Das kfr. Fremdkapital ist hierbei aus der Summe der Aktiva zurückzurechnen. Für das sonstige Umlaufvermögen gilt die Annahme von 25 aus der Aufgabe. Die Differenz aus der Bilanzsumme t = 4 i.H.v. 155 und der hier ermittelten neuen Bilanzsumme i.H.v. 161,238 ist der Kapitalbedarf von 6,238 T€uro.
|
Bleibt die Frage der Bestimmung der Zuverlässigkeit der hier erzielten Ergebnisse. Weil jede Regression stets nur eine Prognose ist, also keinen der bisherigen (oder künftigen) Werte definitiv erklärt, ist dies sinnvoll zu berechnen. Da der angenommene Zusammenhang linear ist, bietet sich die Korrelationsrechnung an. Hier ist zunächst die nebenstehende Hilfstabelle zu ermitteln.
Hierauf ist noch der Mittelwert der X-Reihe von 168,75 und der Mittelwert der Y-Reihe i.H.v. 45,5 zu bestimmten. Sigma X = 15,15544457 und Sigma Y = 3,201562119. Aufgrund dieser Vorbereitung kann man die Korrelation der bisherigen Umsatz- und Warenbestandsgrößen folgendermaßen bestimmen:
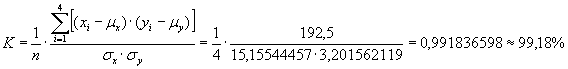
Der statistisch demonstrierbare Zusammenhang ist also mit nahezu K = 1 außerordentlich gut. Die Prognose für t = 5 ist damit stochastisch gesehen sehr zuverlässig. Diese Rechnung ist allerdings wie jede Korrelation lediglich ein Hinweis und kein Beweis. Ein statistischer Beweis existiert nicht, auch wenn Statistiken gerne benutzt werden, um aufgrund angeblicher Zusammenhänge Projekte und Technologien zu be- oder verhindern.
Bleibe eine Anmerkung zum Titel der ganzen Sache, denn der ist außerordentlich ungeschickt gewählt. Dynamische Verfahren sind nämlich eigentlich definiert als mehrperiodige Methoden, die den Zinseszinsfaktor verwenden – wie beispielsweise die Kapitalwertrechnung. Das ist hier aber gerade nicht der Fall. Die Sache "dynamisch" zu nennen trägt also nicht gerade zur Klarheit der Angelegenheit bei. Besser wäre es, von statistischer Kapitalbedarfsprognose zu sprechen, weil statistische Verfahren genutzt werden. Dennoch ist die eine statische Rechnung, weil kein Zinseszinsfaktor vorkommt.
Links zum Thema: Kapitalbedarfsrechnung: unser täglich Brot… | Kundenzahlungszielrechnung: eine neue Prüfungsfalle Vollständige Finanzplanung, Skript | Vollständige Finanzplanung, Excel | Nutzung der Finanzplanung zur Feststellung der Zahlungsunfähigkeit (interne Links)







