Die Mathematik ist bei vielen Aus- und Fortbildungsteilnehmern sehr unbeliebt. Sie gilt als schwierig und wenig realitätsnah. Das ist nicht immer berechtigt: schon mit ganz einfachen Mitteln kann man erschreckend realistische Ergebnisse erzielen. Sehen wir uns mal einen solchen Fall an:
Viele wirtschaftliche Phänomene denken in Rechnungsperioden. Der einer Rechnungsperiode t zugeordnete Wert X sei von mindestens einer anderen, externen Größe a abhängig. Die Formel in unserem Beispiel ist rückkoppelnd, will heißen was heute zum Zeitpunkt t mit X los ist, hängt vom Zustand der Variable X zur Periode t-1 und (mindestens) einem konstanten Änderungsfaktor ab. Zudem muß die Beispielfunktion nichtlinear sein, also mindestens eine Multiplikation enthalten. Im folgenden Beispiel wählen wir den einfachsten denkbaren Fall, nämlich
![]()
Wer das zu abstrakt findet mag sich vorstellen, X sei die Marktpenetration eines bestimmten Gutes. Ist kein einziges Produkt im Markt, gilt X = 0. Sind alle Produkte nur von uns, gibt es also keinen weiteren Anbieter, so gilt X = 1 (entsprechend 100%). Wir setzen jetzt einfach einen willkürlichen Anfangswert von X0 = 0,4 und variieren nur noch die Größe a. Das ist nicht so langweilig wie es auf den ersten Blick scheinen mag.
Wird (ebenso willkürlich) festgelegt a = 0,8, so erhalten wir das Bild eines aussterbenden Marktes. Die Marktpenetration sinkt von 40% gegen null:
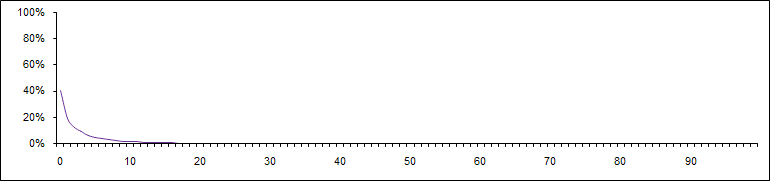
Bei einem a = 2 scheint der Markt stabil zu sein:
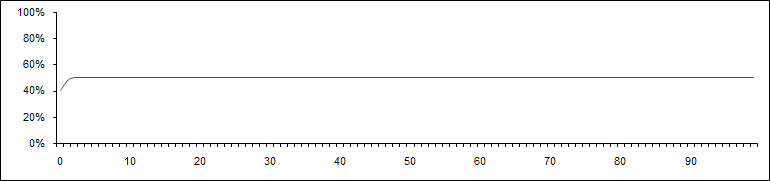
Beides entspricht der alten, auf Adam Smith (1723-1790) zurückgehenden Stabilitätsthese die im wesentlichen besagt, daß ungestörte Märkte von sich aus einen Zustand der Stabilität anstreben. In den beiden vorstehenden Beispielen ist das der Fall – wobei auch das Aussterben eine Art von Stabilität darstellt.
Was aber passiert bei einem (wiederum willkürlichen) a = 3? Überrascht stellen wir eine Oszillation fest, die keine äußeren Ursachen haben kann, denn in unserem Modellmarkt gibt es all die vielen Ursachen, die Märkte angeblich instabil werden lassen, ja gar nicht:
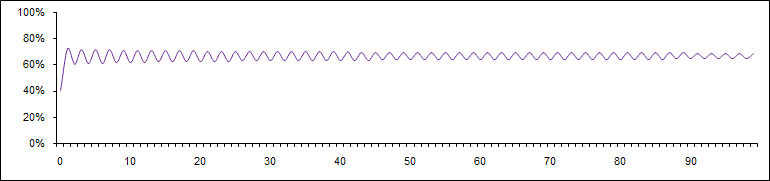
Wir sehen, es ist schon gar nicht mehr so langweilig. Viel spannender wird es aber noch mit a = 3,9. Jetzt erhalten wir nämlich, was man in der Mathematik als Chaoszustand bezeichnet:
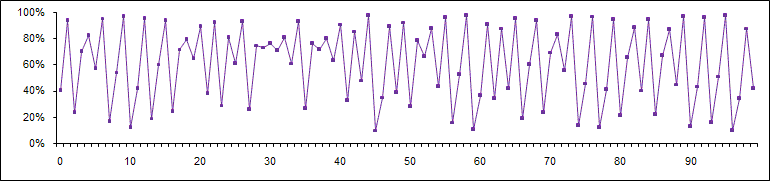
Für diesen Zustand ist charakteristisch, daß eine "wilde" Schwankung über die ganze mögliche Bandbreite entsteht. Dies zu verdeutlichen haben wir in der Grafik Punkte eingebaut. Das Chaos hat aber noch eine andere, viel wichtigere fundamentale Eigenschaft. Die sieht man, wenn man a minimal auf sagen wir mal auf a = 3,900001 verändert. Diese Veränderung im Mikrobereich hat eine dramatische Auswirkung:
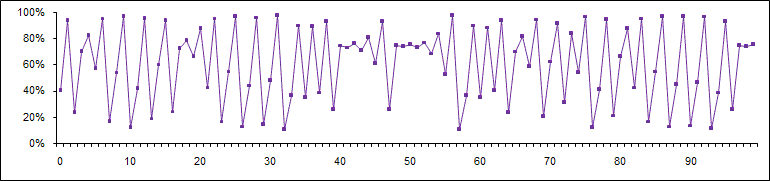
Vergleicht man die beiden vorstehenden Grafiken Schritt für Schritt so stellt man fest, daß die beiden Kurven zu Anfang noch weitgehend deckungsgleich sind, dann aber radikal voneinander abweichen. Die minimale Änderung eines Ausgangswertes, die sowohl bei einem stabilen als auch bei einem oszillierenden Markt keine wahrnehmbare Auswirkung gehabt hätte, führt im Bereich des Chaoszustandes nach wenigen Iterationen zu vollkommen anderen Ergebnissen. Was aber sagt uns das?
Die Grundeigenschaften der Ausgangsformel sind die Multiplikation, also die Nichtlinearität, und daß was in einer Rechnung als Ergebnis herauskommt als Ausgangswert der Folgeberechnung dient, also die Rückkoppelung. Dies ist nicht nur in der Wirtschaft, sondern auch in der Natur häufig. Wir können also grundlegende Feststellungen machen:
- Rückkoppelnde und nichtlineare Systeme kennen einen Chaoszustand, in dem Änderungen von Ausgangswerten schnell viele Zehnerpotenzen überspringen.
- Der Chaoszustand ist unvorhersagbar. Das ist nicht ein Problem der Rechengenauigkeit, sondern ein grundsätzliches Problem. Im Beispiel wird schon nach ca. 50 Schritten die Rechengenauigkeit jeder Tabellenkalkulation gesprengt: Excel® und OpenOffice® rechnen völlig andere Verläufe mit gleichen Ausgangswerten!
Auf den Punkt gebracht kann man also sagen, daß wenn in Hamburg ein Schmetterling flattert, sich in München das Wetter ändert – wenn zumindestens ein solcher Chaoszustand relevant ist. Quantenphysikalische Mechanismen sind damit eben nicht nur ein Problem der Atomphysiker, sondern direkt alltagsrelevant. Dies aber begründet erneut die prinzipielle Unvorhersagbarkeit rückkoppelnder nichtlinearer Systeme, denn Ort und Energie eines Teilchens sind nie gleichzeitig genau zu bestimmen (heisenberg'sche Unschärferelation). Dies ist der Hauptgrund, warum langfristige Wettervorhersagen nicht eine Frage der Modellqualität, sondern prinzipiell unmöglich sind – und warum der Klimaschwindel unwissenschaftlich ist, denn wenn man nicht wissen kann, was in zwei Wochen mit dem Wetter los ist, wie kann man dann genau prognostizieren, was in hundert Jahren mit dem Klima passiert?
Wir sind aber noch längst nicht fertig. Probieren wir ein bißchen weiter mit dem Modell herum und ändern wir den a-Faktor mal auf a = 4,09. Wir erleben ein weiteres mathematisches Phänomen, den Absturz:
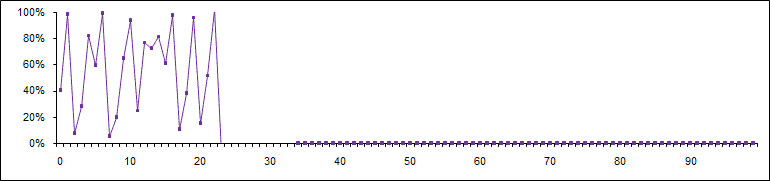
Auf eine anfänglich chaotische Schwankung folgt ein Absturz gegen unendlich. Schon nach 33 Iterationen ist X33 = 10264 und den 34. Wert kann Excel nicht mehr berechnen (dargestellt durch die Punkte auf der Nullinie). Auch das ist für chaotische Systeme typisch: die unvorhersagbare Schwankung kann zu einem Absturz gegen einen unendlichen Wert führen. Dieser Absturz ist gleichsam die potenzierte Unvorhersagbarkeit. Das aber ist der guter Moment, einen Blick in die Börse zu werfen. Schauen wir uns mal den Verlauf des Dow Jones Industrial Average Index börsentäglich seit dem 1. Januar 1990 an:
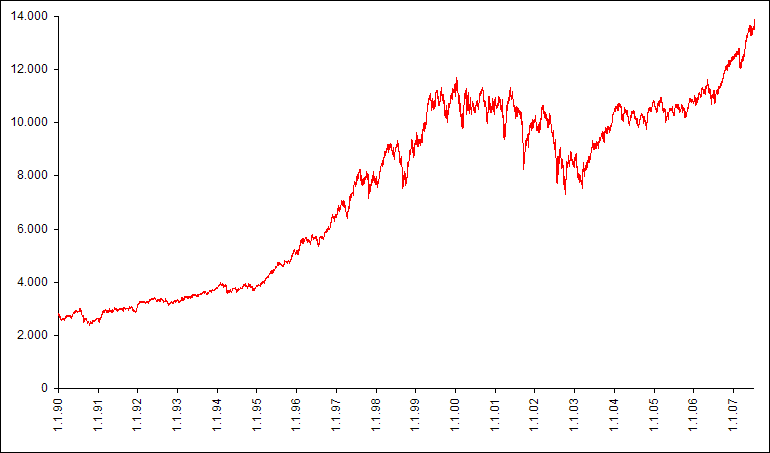
Hier kann man natürlich keine einfache mathematische Beziehung mehr aufmachen. Man kann vermutlich gar keine mathematische Funktion angeben, denn die Verhältnisse an der Börse sind viel komplexer als in unserem eingangs dargestellten Modell. Wie das Beispielmodell ist aber auch die Börse nichtlinear und rückkoppelnd. jeder Markt ist das. Jeder Markt kennt also auch den Chaoszustand und den Absturz. Und wie der aussehen könnte, haben wir vor einigen Tagen hier dargestellt.
Ach ja, spekulieren wir mal am Schluß noch ein wenig. Gestern haben wir dargestellt, warum die Geldmengendefinition der EZB mit M1 bis M3 meiner Meinung nach schlechter ist als die der Schweizer Notenbank mit vier Geldmengen. Dies haben wir insbesondere mit dem Multiplikator zwischen der Bargeldmenge und der Buchgeldmenge auf Sichtkonten erklärt, der im wesentlichen durch die Geldumlaufgeschwindigkeit determiniert ist. Kann das ein Zünder sein, der das gesamtwirtschaftliche System zum Einsturz bringen könnte? Die offensichtliche Geheimnistuerei mancher Zentralbanken läßt den Schluß immerhin zu, aber natürlich ist das nur eine Spekulation 😉
Links zum Thema: Hühner, Gänse und Schweine, oder worum es bei der Hypothekenkrise wirklich geht | Die Geldmengendefinitionen, oder was man vor uns verheimlichen will | Soll ein Krieg das Finanzsystem retten? (interne Links)







