Zu den Kernkompetenzen eines Prüfungsteilnehmers gehört es, die richtige Methode zu finden und unter den Bedingungen knapper Zeit und beschränkter technischer und rechnerischer Mittel anzuwenden. Das bedeutet oft, daß Näherungsverfahren genutzt werden müssen, selbst wenn die in Zeiten der Datenbanken und Tabellenkalkulationsprogramme kein Mensch mehr in der Wirklichkeit mehr verwendet. Schon vorgestern haben wir hierfür ein Beispiel gesehen. Jetzt kommt ein neuer Anwendungsfall ungenauen Rechnens.
So haben wir schon früher gezeigt, wie man eine Anleihe berechnet. Die Methode hat aber den Nachteil, aufwendig zu sein und i.d.R. einen Computer zu erfordern. Wie aber geht man vor, wenn man den Effektivzins einer Schuldverschreibung will, aber keine vollständige Effektivzinsrechnung machen will oder kann? Hier gibt es nämlich eine Abkürzung, die nicht nur in Klausuren praktisch sein kann:
| Rückkaufwert der Anleihe bei Fälligkeit: | 10.000,00 € |
| Emissionskurs der Anleihe: | 9.800,00 € |
| Laufzeit der Anleihe: | 8 Jahre |
| Nominalzins der Anleihe: | 4,5% p.a. |
Für das vorstehende fiktive Papier soll der Effektivzins berechnet werden. Normalerweise müßte man eine Tabelle mit neun Zeilen machen, nämlich der Anfangsinvestition i.H.v. 9.800 Euro, den zehn Zinszahlungen zu je 450 Euro und der Rückzahlung von 10.000 Euro. Die Werte müßten abgezinst und der Effektivzins müßte berechnet werden. Die "klassische" Näherungsmethode funktioniert, ist aber viel zu aufwendig. Eine Hintertür ist hier hochwillkommen:
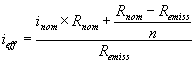
Die Formel sieht auf den ersten Blick vielleicht kompliziert aus, ist aber eigentlich ganz einfach zu benutzen. Mit den eingesetzten Werten aus dem vorstehenden Beispiel ergibt sich:
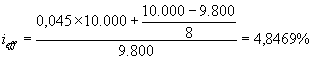
So einfach kann das gehen: wird die Anleihe zu 9.800 Euro emittiert, mit 4,50% p.a. nominal verzinst und nach acht Jahren zu 10.000 Euro zurückgekauft, so ergibt sich ein Effektivzins von näherungsweise ieff = 4,8469%.
|
Dabei wäre die präzise Rechnung viel aufwendiger: nach einer anfänglichen Auszahlung bei t = 0 in Höhe von 9.800 Euro erhält der Investor zunächst sieben Mal die 4,5% auf den Nominalwert i.H.v. 10.000 Euro, also pro Jahr 450 Euro als Zins. Im letzten (achten) Jahr werden nicht nur 450 Euro, sondern auch der nominalwert i.H.v. 10.000 Euro vom Emittenten des Papiers zurückbezahlt. Insgesamt erhält der Investor also 3.800 Euro mehr Einzahlungen als er (anfänglich) auszahlt.
Bekanntlich gibt es für die allgemeine Kapitalwertformel keine generelle Lösung, weil man den Term nicht nach i hin umstellen kann. Die Summe i.H.v. 3.800 Euro ist also iterativ gegen Null zu führen:
![]()
Tut man dies mit einem Computer, so kommt man auf eine Effektivverzinsung der Zahlungsreihe in Höhe von 4,807034%.
Dies ist die einzige präzise Lösung, und damit die einzige praxistaugliche Methode. Vor einer Prüfung ist es aber die falsche Frage, was man in der Wirklichkeit tut, denn dieses Verfahren setzt elektronische Hilfsmittel voraus – die in den meisten Prüfungen nicht zugelassen sind. Die vorstehende Näherungsmethode ist also der einzig gangbare Weg, und liefert zudem ein schnelles Ergebnis mit leidlich guter Genauigkeit.
Links zum Thema: Kapitalwert- und Effektivzinsrechnung: mit einfachen Sachen Freude machen… | Wertpapierrechnen: wie bewertet man eine Anleihe? | Kapitalwert- und Effektivzinsrechnung: die Kosten-Falle | Forum für Betriebswirtschaft | Interner Zinsfußrechner für Excel | Formelsammlung der BWL (interne Links)







