Nachdem wir uns zunächst vor einigen Tagen über die Kostenvergleichsrechnung ausgelassen haben, und dann ein grundlegender Artikel über die Berechnung der kritischen Leistung folgte, betrachten wir heute den beliebtesten Fehler im Zusammenhang mit der Berechnung der kritischen Leistung: die negative kritische Leistung, oder Lernen mit Lücke: wer schematisch nachmacht, und unverstanden imitiert, der stürzt bei diesem Aufgabentyp gnadenlos ab. Auswendiglerner aufgepaßt, das hier ist eine böse Falle:
Kostenverhältnisse und Kostenverläufe
Aufgaben zur Kostenvergleichsrechnung beginnen oft mit einer umfangreichen Fallschilderung und vielen Einzelinformationen. Das haben wir schon im ersten Beitrag dieser Serie betrachtet, so daß wir das nicht wiederholen. Hier sparen wir uns alle Berechnungen, und beginnen mit den Ergebnissen einer Kostenveregleichsrechnung. Diese finde für zwei Maschinen die folgenden Daten:
| Nr. | Posten | Anlage A | Anlage B |
| 01. 02. 03. |
Fixkosten variable Kosten Maximale Ausbringungsmenge (Kapazitätsgrenze) |
30.000,00 €/Jahr 6,00 €/Stück 10.000 Stück/Jahr |
40.000,00 €/Jahr 4,00 €/Stück 10.000 Stück/Jahr |
Die glatten Zahlen erleichtern hier auch die Rechnung, denn viele Fallen verstecken sich in unübersichtlichem Zahlenwerk. Wie so oft macht es auch hier Sinn, sich zunächst eine kleine Skizze der Kostenverläufe anzufertigen. Für Ausbringungsmengen von null bis 10.000 Stück/Jahr sieht das folgendermaßen aus:
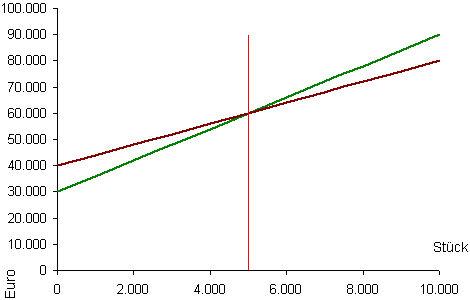
Die Kostenverläufe für Anlage A und Anlage B beginnen bei einer Ausbringungsmenge von null (also bei Stillstand) bei 30.000 Eurobzw. bei 40.000 Euro und steigen dann wegen der unterschiedlichen variablen Stückkosten auch unterschiedlich steil an. Der Schnittpunkt der beiden Kostenlinien markiert die kritische Leistung von 5.000 Stück/Jahr.
Der bekannte Rechenweg
Die kritische Leistung ist der Punkt der Kostengleichheit. Wir wissen aber, daß die um 10.000 Euro/Jahr höheren Fixkosten der Anlage B durch die um 2 Euro/Stück niedrigeren variablen Kosten der Anlage B finanziert werden. Man kann die kritische Leistung also berechnen, indem man die Differenz der Fixkosten durch die Differenz der variablen Kosten dividiert:
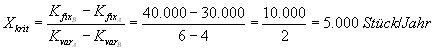
Wer sich jetzt zufrieden zurücklehnt und glaubt, es verstanden zu haben, begeht einen schweren Fehler. Der Haken bei dieser Sorte von Aufgaben liegt nämlich in den Einzelheiten. Betrachten wir mal einen geringfügig veränderten Fall, bei dem wir das Problem ein wenig verstecken, genau so, wie es auf Prüfungspoeten so gerne tun:
Böse Falle!
| Nr. | Posten | Anlage A | Anlage B |
| 11. 12. 13. 14. 15. |
Kalkulatorische Abschreibung Kalkulatorische Zinsen Sonstige (zahlungsgleiche) Fixkosten variable Kosten Maximale Ausbringungsmenge (Kapazitätsgrenze) |
18.000,00 €/Jahr 10.000,00 €/Jahr 3.000,00 €/Jahr 6,00 €/Stück 10.000 Stück/Jahr |
12.000,00 €/Jahr 8.000,00 €/Jahr 5.000,00 €/Jahr 4,00 €/Stück 10.000 Stück/Jahr |
Der Auswendiglerner wendet Dinge, die er gepaukt hat, schematisch an. Beispielsweise werden die Fixkosten aus diesen Ausgangsdaten addiert, und in die vorstehende Formel eingesetzt. Das ergibt das folgende überraschende Ergebnis:
![]()
Huch, eine negative kritische Leistung? Wie kann eine Anlage –3.000 Stück pro Jahr produzieren? Ein solches Ergebnis wird oft für einen Fehler gehalten, ist aber keiner. Eine Skizze zeigt, daß der Schnittpunkt der beiden Kostengeraden tatsächlich unter null liegt:
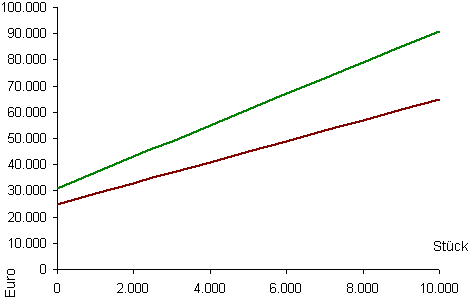
Doch nicht alles, was mathematisch richtig ist, ist auch ökonomisch sinnvoll: hier ist die kritische Leistung nämlich undefiniert. Allgemein muß man nämlich berücksichtigen, daß eine kritische Leistung nur definiert ist, wenn KfixA < KfixB und KvarB < KvarAoder umgekehrt KfixB < KfixA und KvarA < KvarB. Etwas weniger formal gesagt bedeutet dies, daß bei einer Anlage die Fixkosten pro Jahr geringer sein müssen und bei der anderen Anlage die variablen Kosten pro Stück niedriger sein müssen. Im ersten Beispiel war das der Fall, aber im zweiten Beispiel hatte Anlage A mit 31.000 Euro/Jahr die höheren Fixkosten, aber mit 6 Euro/Stück auch die höheren variablen Kosten. In diesem Fall ist eine kritische Leistung undefiniert.
Das Problem wäre noch vergleichsweise offenbar, wenn nicht in den Zeilen 11 bis 15 Ausgangsdaten geboten worden wären, die erst addiert werden müssen. Im allseits bekannten Klausurstreß handeln dann viele Prüfungskandidaten schematisch und setzen einfach Zahlenwerte ein. Das aber ist ein Fehler: man soll nie etwas tun, weil es früher schon mal richtig war, sondern stets jede Handlung individuell beurteilen. Das ist nicht nur im Leben so, sondern auch in der Prüfung. Denn wir alle wissen: nicht für das Leben, sondern für die Prüfung lernen wir… oder so ähnlich! 🙂
Links zum Thema: Investitionsrechnung: so macht man eine Kostenvergleichsrechnung | Investitionsrechnung: wenn die Leistung kritisch wird… | Übersicht: Die wichtigsten Verfahren der Investitionsrechnung | Kostenvergleichsrechnung: wie man Preise drückt und Lieferanten knebelt | Prüfungsrelevant: Grundgedanken und Kostenverläufe der Break-Even-Rechnung (interne Links)








Sehr gut erklärt ! Jedoch eine Frage:
Was ist wenn die variablen Kosten beider Varianten gleich sind?
Dann subtrahiere ich 2 gleiche Zahlen und erhalte 0.
Allerdings ist es ja mathematisch nicht möglich durch 0 zu teilen.
Ist dann die kritische Menge ebenfalls undefiniert?
LG
Vielleicht doch mal im Forum fragen, denn der Autor ist leider bereits 2009 verstorben.