Im Bereich der dynamischen Investitionsrechnung (Übersicht) gehört die interne Zinsfußrechnung zu den häufigsten Verfahren, denn mit dieser Methode kann man die in einer Rente enthaltene tatsächliche Verzinsung bestimmen: nützlich für die den Banken durch §6 Abs. 1 PAngV vorgeschriebene Effektivzinsrechnung, aber auch, den tatsächlichen Zins eines Leasingvertrages nachzurechnen (Leasingzinsrechner für Excel). Leider wird in kaufmännischen Prüfungen aller Art bis heute noch immer ein Näherungsverfahren angewandt, das in der betrieblichen Realität niemand mehr anwendet.
Ein Beispiel zeigt, was gemeint ist. Ein Investor erwirbt eine Anlage im Wert von 50.000 Euro. Mit dieser Anlage werden verkaufsfähige Produkte hergestellt, d.h. die Einzahlungen lassen sich der Anlage zurechen (was eine Voraussetzung für die Anwendung dynamischer Methoden ist). In den folgenden vier Jahren, die die Anlage voraussichtlich nutzbar sein wird, betragen die prognostizierten Einzahlungen 15.000 Euro, 22.000 Euro, 18.000 Euro und 10.000 Euro. Die anschließende Verschrottung der Maschine kostet voraussichtlich nichts. Die Effektivverzinsung ist zu finden – eine häufige Fallkonstellation in Übungen, Prüfungen und sogar in der betrieblichen Realität.
In den meisten kaufmännischen Prüfungen wird bei solchen Aufgaben erwartet, daß der Prüfungsteilnehmer zunächst den Kapitalwert der Investition mit zwei "Versuchszinsen" berechnet, wobei ein Ergebnis positiv und das andere negativ sein soll (aber nicht zwingend muß). Das könnte folgendermaßen aussehen:
| t | Et – At | C0 i = 10% |
C0 i = 15% |
| 0 | –50.000,00 € | –50.000,00 € | –50.000,00 € |
| 1 2 3 4 |
15.000,00 € 22.000,00 € 18.000,00 € 10.000,00 € |
13.636,36 € 18.181,82 € 13.523,67 € 6.830,13 € |
13.043,48 € 16.635,16 € 11.835,29 € 5.717,53 € |
| Summe | +15.000,00 € | +2.171,98 € | –2.768,54 € |
Es muß grundsätzlich klar sein, wie man mit Hilfe der Barwertrechnung zu den einzelnen C0-Ergebnissen kommt. Natürlich werden die Werte kleiner, wenn der Zins ansteigt. In vielen Aufgaben wird verlangt, eine Skizze wie diese hier zu fertigen:
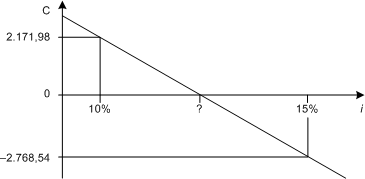
Der interne Zins (oder Effektivzins, das ist dasselbe) ergibt sich an der Stelle, an der die Linie, die die beiden rechnerisch gefundenen Ergebnisse miteinander verbindet, die Nullinie des Koordinatensystems schneidet. Die allgemeine Definition ist also:
![]()
Leider ist diese Formel unlösbar, weil es keine (einfache) Möglichkeit gibt, nach i hin umzustellen – denn der Zins i steht ja hinter der Summe. Es gibt also, von wenigen Ausnahmen abgesehen, keine exakte Lösung. Die jetzt oft verlangte Näherungsmethode ist ein Interpolationsverfahren, das die Fläche der beiden unter bzw. über der Nullinie entstehenden Dreiecke vergleicht:
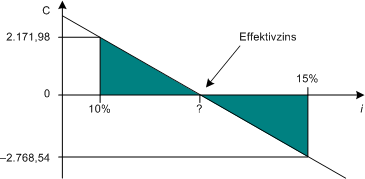
Hierfür muß der Prüfungsteilnehmer, der mit den beiden Versuchszinsen zunächst die beiden Kapitalwerte berechnet hat, die Interpolationsformel auswendig kennen oder nachschlagen können:
![]()
Jetzt sind die beiden Ergebnisse einzusetzen, die in Prüfungsaufgaben sogar oft vorgegeben sind. Das führt zur folgenden Lösung:
![]()
Kaum jemand kommt auf die Idee, dieses Ergebnis nachzurechnen. Das wundert nicht, denn in Prüfungen fehlt immer die Zeit. Wir machen uns jetzt aber doch die Mühe. Verwendet man den Effektivzins als Kalkulationszins, dann muß ja gemäß der vorstehenden Definition ein Kapitalwert i.H.v. C = 0 herauskommt. Tatsächlich aber kommt eine Überraschung heraus:
| t | Et – At | C0 i = 12,19813% |
| 0 | –50.000,00 € | –50.000,00 € |
| 1 2 3 4 |
15.000,00 € 22.000,00 € 18.000,00 € 10.000,00 € |
13.369,21 € 17.476,38 € 12.744,29 € 6.310,41 € |
| Summe | +15.000,00 € | –99,72 € |
Diese Abweichung mag für Prüfungszwecke zu ignorieren sein, denn der Teilnehmer soll nur demonstrieren, daß er mit dem Verfahren umgehen kann. Für reale Anwendungen ist dieses Ergebnis unbrauchbar. Allgemein ist die Abweichung aber leicht erklärt: wer sich noch mehr Mühe macht, und den Verlauf des Kapitalwertes in Abhängigkeit vom Zins exakt zeichnet, stellt eine beträchtliche Abweichung zwischen Näherung und realem Verlauf fest:
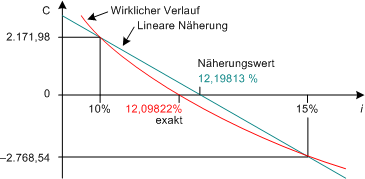
Die Sache ist in Computerskizzen oft schlecht zu sehen; in der vorstehenden Skizze wurde die Abweichung netwas übertrieben, um sie sichtbarer zu machen. Es ist aber unschwer unter Beweis zu stellen, daß der Wert von ieff = 12,098219838% die präzise interne (effektive) Verzinsung darstellt. Man muß nur erneut nachrechnen:
| t | Et – At | C0 i = 12,09822% |
| 0 | –50.000,00 € | –50.000,00 € |
| 1 2 3 4 |
15.000,00 € 22.000,00 € 18.000,00 € 10.000,00 € |
13.381,12 € 17.507,54 € 12.778,40 € 6.332,94 € |
| Summe | +15.000,00 € | ±0,00 € |
Erst jetzt ist der wirkliche Effektivzins erreicht. Dies ist die tatsächliche interne Verzinsung, die die Zahlenreihe bietet. Dieser Wert ist nicht, oder jedenfalls nicht mit vertretbarem Aufwand, durch die Näherungsmethode zu finden, sondern nur im Wege der Zielwertsuche. Die beherrschen heute schon bessere Taschenrechner – oder man muß eine VBA-Codezeile in Excel® schreiben. Das aber ist noch immer nicht Prüfungsgegenstand, denn die meisten Prüfungen werden zwar mit Formelsammlung aber ohne Computer geschrieben, noch immer. So unterscheiden sich Theorie und Praxis, so lernt man noch immer für die Prüfung statt fürs Leben. Auch im Rechnungswesen!
Einen allgemeinen Kapitalwertrechner zum Ausprobieren und Nachrechnen findet der Leser hier. Ein spezieller Vergleichsrechner, der die hier dargestellte Ungenauigkeit visualisiert, wird nur hier angeboten (nicht auf der Zingelseite erhältlich). Aktivieren Sie die Makros, um die Dateien auszuprobieren. Beide Excel-Dateien für Excel® 97 bis 2007 sind uneingeschränkt funktionsfähig aber Kennwörter für Einblick in Formeln und VBA-Code nur für registrierte BWL CD Nutzer verfügbar.
Links zum Thema: Grundbegriffe: statische und dynamische Methoden | Übersicht: Die wichtigsten Verfahren der Investitionsrechnung | Interner Zinsfuß: eine hammerharte Prüfungs-Knallschote | Kapitalwertrechner | Leasingrechner (interne Links) Rechenbeispiel interner Zinsfuß (externer Link)







