Klausurfragen im Bereich der Statistik richten sich oft auf Zusammenhangmaße, mit denen der Grad der wechselseitigen Abhängigkeit zwischen zwei Merkmalen erforscht werden soll. Viele Teilnehmer lernen die zugrundeliegenden Definitionen und mathematischen Verfahren ganz genau – und tappen dann in eine einfache Falle, die hinterhältige Aufgabenersteller mit Vorliebe in Klausuren und Prüfungen plazieren. Schauen wir mal, wie das aussehen kann:
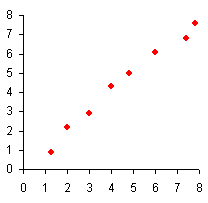
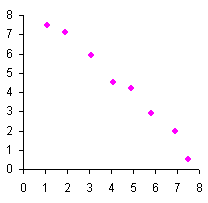
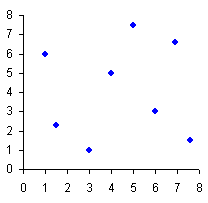
Zwei metrisch skalierte Merkmalsausprägungen werden erhoben, im Beispiel (der Übersichtlichkeit halber) nur in kleiner Anzahl. Jeder Punkt repräsentiert zwei Merkmalsausprägungen, je eine auf der horizontalen und eine auf der vertikalen Achse.
Hierbei ist augenfällig, daß im linken Fall der Zusammenhang zwischen beiden Merkmalen groß zu sein scheint: steigt eine der Merkmalsausprägungen, so führt dies auch zum Anstieg der anderen Merkmalsausprägung. Man spricht von einer hohen Korrelation (exakt: K = 99,18%). Nicht anders ist es im mittleren Fall: auch das ist ein hoher Zusammenhang, aber in der Weise, daß beim Anstieg einer der beiden Merkmalsausprägungen die andere Merkmalsausprägung eher sinkt. Man spricht von einer negativen Korrelation (im Beispiel beträgt diese K = –99,12%). Im rechten Beispiel schließlich verteilen sich die Punkte über die ganze Fläche: das spricht gegen einen Zusammenhang. Aus der Änderung einer Merkmalsausprägung kann nicht auf Veränderungen der jeweils anderen Merkmalsausprägung geschlossen werden. Die Korrelation zwischen den beiden Merkmalen ist klein (im Beispiel nur2,25%). So weit der formale, d.h. rechnerische Teil. Den zu beherrschen reicht freilich noch nicht…
Die Statistik versucht, aus numerischen Ergebnissen Aussagen über die Grundgesamtheit abzuleiten, also aus Einzelbeobachtungen Aussagen über die Wirklichkeit herzuleiten. Das kann sinnvoll sein, oder auch nicht, denn der augenfällige Zusammenhang im linken und im mittleren Beispiel verführt zu unzulässigen Schlüssen. Das wissen die politischen Demagogen und behaupten, nur aus der Statistik die Wirkung von Kernkraftwerken auf Leukämie oder Umweltgiften auf unser Wohlbefinden herleiten zu können. Wie absurd eine solche rein statistische Argumentation ist offenbart sich nämlich erst, wenn man die Achsen beschriftet. Hinterlistiger weise haben wir das oben unterlassen. Holen wir das jetzt doch einfach mal nach:
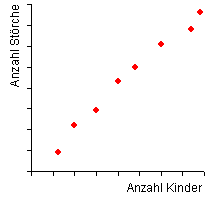
Der hohe Zusammenhang zwischen den beiden Merkmalen ist ja oben recht augenfällig gewesen. Also kann der Leser jetzt, da er die erhobenen Sachverhalte kennt etwas lernen: Mehr Störche, mehr Kinder. Der Storch bringt also die Kinder…
Winston Churchill wird das Zitat nachgesagt, man solle keiner Statistik glauben, die man nicht selbst gefälscht habe. Doch einer Fälschung bedarf es oft gar nicht: nur die "richtige" Präsentation von Daten reicht aus, einen falschen Schein zu erzeugen – die Ökologisten, die Lobbyisten und viele andere mehr wissen das ganz genau.
Fragt ein Aufgabenlyriker also, was mit dem Ergebnis einer hochgradigen Korrelation bewiesen sei, so ist die Antwort natürlich immer – nichts. Eine Korrelation alleine beweist gar nichts. Sie muß immer mit außerstatistischen Belegen untermauert werden oder ist an sich wertlos.
So mag der Leser sich also mit dem Fernglas auf die Lauer legen, und nicht nur die Kinder und die Störche zählen: er muß auch einen Storch mit Baby am Schnabel im Landeanflug auf das Schlafzimmer beobachten. Dann kann aus Korrelation und Beobachtung der Wirklichkeit ein Beweis errichtet werden. Gelingt eine solche Beobachtung nicht, ist die Statistik für sich genommen ziemlich aussagelos. Und zwar auch ohne Fälschung und bei völlig korrekter formaler und mathematischer Vorgehensweise. Eine Statistik liefert nur Hinweise, nie Beweise. Sie ist Grund für weitere Forschungen aber niemals selbst die einzige Untersuchung. Das kann man meines Erachtens nach nicht oft genug betonen – in Lehrveranstaltungen ebenso wie in politischen Debatten.
Links zum Thema: Nominal, ordinal und metrisch: kleine Übersicht über die Datentypen der Statistik | Gauß ohne Schrecken: so funktioniert das Rechnen mit der Normalverteilung (Teil 1-3) | Teil 2-3 | Teil 3-3 | Gauß-Rechner für Excel | Formelsammlung der Betriebswirtschaft (interne Links)







