(Teil 1-3)
In betriebswirtschaftlichen Zusammenhängen muß immer wieder mit der Normalverteilung gerechnet werden, denn normalverteilte Merkmalsausprägungen sind häufig: technische Maße etwa im Qualitätsmanagement, aber auch Nachfragedaten, Wartezeiten von Kunden oder Kosten- und Leistungskennzahlen sind oft normalverteilt. Das Rechnen mit der gauß’schen Verteilungsfunktion birgt für viele Studienteilnehmer aber manchen Schrecken. Das muß nicht sein, wie wir in dieser dreiteiligen Serie zeigen werden.
Um diesen Artikel (und die folgenden beiden) Beiträge nachzuvollziehen, ist diese Tabelle erforderlich. Der Leser sollte sie sich ggfs. ausdrucken. Wird ein elektronischer Gauß-Rechner benutzt, können die Ergebnisse leicht abweichen (präziser). Das ist jedoch nicht weiter schlimm: hier kommt es auf das Verständnis des Prinzipes an. Und in Klausuren muß ohnehin meist mit Tabellen gearbeitet werden.
Die grundlegende Gesetzmäßigkeit
Zunächst ist bedeutsam zu erkennen, daß die sogenannte gauß’sche Glockenkurve eine Dichtefunktion ist. Sie zeigt die Wahrscheinlichkeit (P) des Eintretens eines metrisch skalierten Ereignisses in Abhängigkeit von der Standardabweichung (Sigma) vom Mittelwert an:
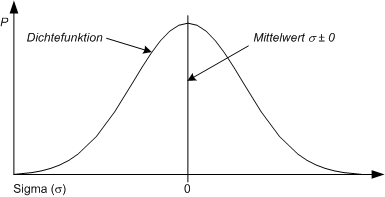
Genau am Mittelwert ± 0 Sigma, also am Scheitelpunkt der Kurve, ist das Eintreten zukünftiger Ereignisse am wahrscheinlichsten. Je weiter man sich nach oben (rechts) oder unten (links) vom Mittelwert entfernt, desto unwahrscheinlicher wird das Eintreten neuer Ereignisse.
| Beispiel: Täglich werden durchschnittlich 500 Stück eines Produktes nachgefragt (metrisch skaliertes Merkmal: Nachfrage). Der Mittelwert der Merkmalsausprägung ist also 500. Die mittlere Abweichung (Standardabweichung, Sigma) betrage 60 Stück. Es gilt also 500 ± 60 Stück für die Nachfrage. Die Wahrscheinlichkeit, daß am nächsten Tag wiederum genau 500 Stück nachgefragt werden, ist am größten (Scheitelpunkt der Kurve). Die Wahrscheinlichkeit, daß es aber 501, 502, 503 usw. oder ebenso 499, 498, 487 usw. Stück sind, sinkt jeweils (abfallende Seiten der Kurve). |
Wie man die gauß’sche Glocke läutet
Das Schöne an der gauß’schen Gesetzmäßigkeit ist, daß sie verallgemeinert werden kann. Sie gilt für eine Vielzahl von möglichen Merkmalen: Wartezeiten in der Kassenschlange, Abmessungen maschinell produzierter Teile, Anzahl nachgefragter Produkte – sie alle kann man mit dem gleichen, auf Carl Friedrich Gauß (1777-1855) zurückgehenden mathematischen Modell berechnen. Genau das zeigt die oben verlinkte Tabelle, die sich der fleißige Leser ja gewiß schon angeschaut hat. Diese zeigt nämlich den Flächenanteil der Grafik zwischen Mittelwert und einem bestimmten Sigma-Wert:
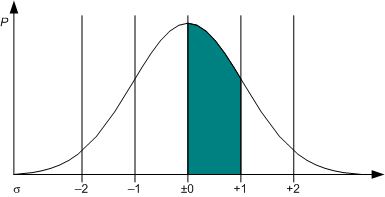
Man schlage in dieser Tabelle jetzt den Wert für 1,00 Sigma nach. Der gefundene Wert i.H.v. 34,13447% besagt, daß zwischen dem Mittelwert und Mittelwert + 1,00 Standardabweichungen (Sigmas) genau 34,13447% der Fälle zu erwarten sind.
| Beispiel: Ist der Mittelwert der Nachfrage 500 Stück und die mittlere Abweichung (Standardabweichung, Sigma) 60 Stück, so ist die statistisch zu erwartende Wahrscheinlichkeit, am nächsten Tag genau zwischen 500 und 560 Stück zu verkaufen, 34,13447%. |
Das sagt uns freilich noch viel mehr: da die Kurve symmetrisch ist, ist die Wahrscheinlichkeit, bis 500 Stück zu liegen, genau 50%. Die Wahrscheinlichkeit, darüber zu liegen, ist ebenfalls genau 50%. Die Wahrscheinlichkeit, im vorstehenden Beispiel mehr als 560 Stück zu verkaufen, muß aber bei 50% – 34,13447% = 15,86553% liegen.
Der Leser ahnt, daß damit eine Menge wunderbarer Dinge möglich sind. Wie man also die gauß’sche Glocke läutet, zeigen wir in den nächsten beiden Folgen dieser kleinen Serie von Beiträgen, die jedoch diesen Artikel voraussetzen werden.
(Teil 2-3)
Im vorigen Artikel dieser kleinen Serie haben wir demonstriert, wie die gauß’sche Dichtefunktion grundsätzlich funktioniert. In diesem Artikel läuten wir erstmals die gauß’sche Glockenkurve – an einem materialwirtschaftlichen Beispiel. Der Leser sollten die zugrundeliegende Tabelle Gauß’sche Normalverteilung zur Hand haben, um der Rechnung folgen zu können.
Im bereits eingeführten Beispiel waren wir davon ausgegangen, daß die – als normalverteilt angenommene – Nachfrage nach einem Artikel durchschnittliche pro Tag 500 Stück bei einer Standardabweichung von Sigma ± 60 Stück betrage. Das ist zunächst noch etwas theoretisch. Der Lagerbetreiber habe aber nur Lagerraum für maximal 600 Produkte pro Tag. Es kann nur ein Mal pro Tag angeliefert werden. Wenn also mehr als 600 Stück nachgefragt werden, so tritt Lieferunfähigkeit ein, weil das Lager leer ist. Wie groß ist das Risiko, daß dies passiert?
Die Normalisierung
Dies kann mit der gauß’schen Normalverteilungsfunktion berechnet werden, aber man muß erst die Stück in Sigmas umrechnen. Dieser Vorgang heißt Normalisierung. Soll ein Grenzwert i.H.v. Xmax = 600 Stück berechnet werden, so ist hiervon der Mittelwert von 500 Stück abzuziehen und diese Differenz durch den Wert eines Sigmas zu teilen:
![]()
Die Grenze der Lagerkapazität i.H.v. Xmax = 600 Stück liegt also bei Mittelwert + 1,67 Standardabweichungen. Der Bereich oberhalb dieser Grenze ist das Risiko der Lieferunfähigkeit, das dem Flächenanteil des markierten Teiles der Kurve an der ganzen Kurve entspricht:
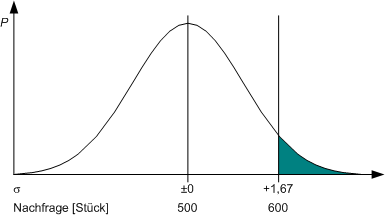
So, und jetzt läuten wir die gauß’sche Glocke, und das geht ganz einfach: wir schlagen in der bekannten (oben verlinkten) Tabelle den Wert für 1,67 Sigma nach und finden einer Wahrscheinlichkeit i.H.v. 45,25403%. Dies ist die Wahrscheinlichkeit einer Nachfrage zwischen 500 und 600 Stück. Wir wollen aber wissen, wie hoch die Wahrscheinlichkeit ist, über 600 Stück pro Tag zu liegen. Also ziehen wir den Ergebniswert aus der Tabelle einfach von eienr Hälfte der Kurve, also von 50% ab, und erhalten für das Risiko der Lieferunfähigkeit einen Wert von 4,74597%.
Dieses war der erste gauß’sche Glockenschlag: das Auffinden der Wahrscheinlichkeit zu einem gegebenen Grenzwert. Im nächsten und letzten Beitrag dieser Serie schauen wir uns das Gegenteil an: wie findet man den Grenzwert, wenn ein (maximales) Risikoniveau gegeben ist?
(Teil 3-3)
Nachdem wir im ersten Artikel dieser kleinen Serie die gauß’sche Glockenkurve grundsätzlich eingeführt haben, läuteten wir im zweiten Artikel zum ersten Mal die gauß’sche Glocke, indem wir herausfanden, wie man das zu einem gegebenen Grenzwert gehörende Risiko findet. In diesem letzten Beitrag dieser Serie sehen wir, wie man für ein gegebenes Risiko einen zugehörigen Grenzwert identifiziert, läuten wir die Glocke also genau anders herum. Auch zu diesem Artikel sollte der Leser die zugrundeliegendeTabelle zur Hand haben, um der Rechnung folgen zu können.
Wir haben festgestellt, daß bei einer mittleren Nachfrage i.H.v. 500 Stück pro Tag und einer Lagerkapazität von Xmax = 600 Stück das Risiko der Lieferunfähigkeit bei Mittelwert + 1,67 Standardabweichungen = 50% – 45,25403% = 4,74597% liegt. Dies sei dem Lagerbetreiber zu groß. Das Lager soll so vergrößert werden, daß das Risiko der Lieferunfähigkeit bei maximal 2% liege. Wie groß muß der zu schaffende Lagerraum hierfür sein?
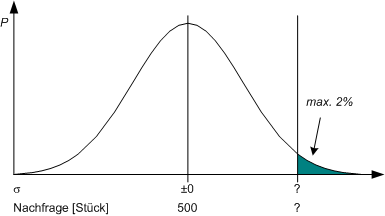
Wir konsultieren also wiederum die bereits bestens bekannte Tabelle, und erinenrn uns, daß diese ja den Bereich vom Mittelwert bis zu einem gegebenen Sigma-Abstand zeigt. Wenn das Risiko der Lieferunfähigkeit unter 2% gedrückt werden soll, ist der erste Tabellenwert über 48% zu aufzufinden. Dieser beträgt 48,03007% und gehört zu 2,06 Sigmas. Wir wissen jetzt also, daß 2,06 Standardabweichungen (Sigmas) über dem Mittelwert die 48%-Grenze liegt. Ein Sigma entspricht aber 60 Stück. Addiert man also einfach 500 + 2,06 x 60 = 623,6 Stück, so hat man die 48%/2%-Grenze:
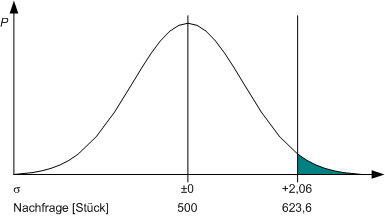
Im Bereich von 500 Stück bis 623,6 Stück liegen also 48% der Fälle (oder von null bis 623,6 Stück/Tag liegen 98% der Fälle, denn die Glockenkurve ist ja symmetrisch). Nur in weniger als 2% der Fälle (genau: in 1,96993% der Fälle) werden mehr als 623,6 Stück pro Tag nachgefragt. Der verfügbare Lagerraum müßte also von 600 auf ca. 624 Stück erhöht werden, um ein Risiko der Lieferunfähigkeit von unter 2% zu erreichen.
Es ist nicht so schwer, aber sehr prüfungswichtig
Wer so also die gauß’sche Glocke läutet, sollte Erfolg in einschlägigen Prüfungen und Klausurarbeiten haben. Es wird empfohlen, mit dem Gauß-Rechner für Excel ein wenig herumzuprobieren. Die damit erzielten Ergebnisse weichen leicht von den hier dargestellten Zahlen ab, weil sie nicht gerundet sind (wie die Werte der Tabelle). Wichtig ist, ein grundlegendes Verständnis für die beiden Rechenwege zu entwickeln, denn Klausurfragen sind oft so gestellt, daß man erstmal herauskriegen muß, was die Aufgabenersteller eigentlich wollen. Hat man die Sache aber erstmal in die Tiefe hinein durchschaut, dann stellt sie in keinem Fall mehr eine echte Hürde dar.
Links zum Thema
Tabelle der gauß’schen Normalverteilung
Gauß-Rechner für Excel
Formelsammlung der Betriebswirtschaft







