Auf unseren Artikel über arg fehlerhafte Berechnungsmethoden bei Lagerumschlagshäufigkeit und Lagerdauer in zahlreichen Lehrbüchern für Auszubildende vom vergangenen Mittwoch sind sehr viele Antworten eingegangen. Zeitweise war ich wegen der großen Zahl von Mails nicht mehr in der Lage, zu antworten. Wir fassen daher in diesem Artikel die wichtigsten Einwendungen zusammen und zeigen, daß unsere These nicht falsifiziert wurde.
Einwendung 1: Die in dem Artikel benutzte Berechnungsmethode für den durchschnittlichen Bestand ist zu theoretisch.
Erwiderung 1: Wir haben in dem Zahlenbeispiel den Durchschnittsbestand aufgrund eines Eisernen Bestandes von 80 und einer Bestellmenge von 20 auf folgende Art und Weise berechnet:
Zweifellos ist dies eine Vereinfachung. Wir müssen aber vereinfachen, um den in dem Artikel darzustellenden Sachverhalt klarzustellen. Es ist besser, den Durchschnittsbestand durch tägliche oder noch häufigere Bestandserhebungen (etwa im Rahmen einer permanenten Buchinventur) zu ermitteln. Dies ist zwar viel komplizierter, führt aber in unserem Kontext zum gleichen Ergebnis. Beide Berechnungsmethoden, unsere und die fehlerhafte Methode aus den Lehrbüchern, benutzen den gleichen (auch willkürlich anzunehmenden) Ausgangswert für den Durchschnittsbestand. Nur der Unterschied zwischen den beiden Methoden soll demonstriert werden. Die Berechnungsmethode für ØBest ist damit unerheblich. Es ginge selbst mit einer willkürlichen Annahme ohne jede Berechnung.
Einwendung 2: Jemand schreibt: "Bei Deiner Formel für LU stellst Du den Verbrauch (10, die 360 sind ja konstant) in ein Verhältnis zu Eiserne Reserve plus Bestellmenge (das Verhältnis der beiden ist dabei in Deiner Formel egal, das Verhältnis zwischen EB und M könnte bei dir auch umgekehrt sein, oder einen der beiden einzelwerte 0, es käme der gleiche Wert heraus): hier also 1/10 = 10% pro Tag. Bei der anderen "falschen" Formel ist dagegen der Wert von LU sehr wohl vom Verhältnis von EB und M abhängig, da beide in der Berechnung des Durchschnittsbestandes nicht gleich gewichtet sind (ob du 2EB + M oder EB + HB rechnest, ist egal, da ja HB als EB + M definiert wird) Hier käme bei einem EB = 0 und M = 100 ein Durchschnittsbestand von 50 heraus, bei EB = 100 und M = 0 ein Durchschnittsbestand von 100 heraus, bei EB = 50 und M = 50 ein Durchschnittsbestand von 75".
Erwiderung 2: Diese Argumentation finde ich verworren und falsch. Ein Verhältnis zwischen EB und M ist unerheblich (meine Gesetzmäßigkeit stimmt für alle Verhältnisse zwischen EB und M). Nur bei EB = 0 funktioniert die Lehrbuchmethode; ist EB > 0, so erbringt die Lehrbuchmethode zu lange Werte für die maximale Lagerdauer. Die folgende Tabelle beweist dies:
| Allgemein | Unsere Lösung | Falsche Lehrbuch-Lösung | |||||||
| EB | ØBest |  |
 |
 |
 |
 |
|
||
| 80 | 90 | 36,00 | 5,00 | 10,00 | 40,00 | 9,00 | 18,00 | ||
| 60 | 80 | 36,00 | 5,00 | 10,00 | 45,00 | 8,00 | 16,00 | ||
| 40 | 70 | 36,00 | 5,00 | 10,00 | 51,43 | 7,00 | 14,00 | ||
| 20 | 60 | 36,00 | 5,00 | 10,00 | 60,00 | 6,00 | 12,00 | ||
| 0 | 50 | 36,00 | 5,00 | 10,00 | 72,00 | 5,00 | 10,00 | ||
Man beachte hier, daß EB + M = HB und damit immer 100 ist. Die Lagerumschlagshäufigkeit hat damit nichts mit der Bestellmenge zu tun, wenn, wie in dem zugrundeliegenden Artikel graphisch skizziert, M um eben soviel abnimmt wie EB zunimmt, denn es wird ja stets der gleiche Höchstbestand abgebaut (und damit umgewälzt). Schon hier offenbart sich, daß die Lehrbuchmethode falsch sein muß, weil die Lagerumschlagshäufigkeit sich nicht ändern darf, wenn öfter geringere Mengen bestellt werden, aber Verbrauch und Höchstbestand konstant bleiben!
Einwendung 3: Daß du in deinem Zahlenbeispiel auf recht ähnliche Werte LU richtig = 36 statt LU falsch = 40 kommst, ist also anscheinend eher Zufall.
Erwiderung 3: Die vorstehende Tabelle beweist, daß das nicht der Fall ist.
Einwendung 4: Man könne mein Postulat falsifizieren, wenn man EB + M oder V variiert. Insbesondere nimmt jemand ein EB + M = 100 aber ein V = 100 pro Tag an. Die maximale Lagerdauer beträgt nun in beiden Rechenverfahren genau 1 Tag (der Leser mag dies selbst nachrechnen, wenn er möchte).
Erwiderung 4: Dies widerlegt meine Theorie keineswegs, denn wenn HB = 100 und Tagesverbrauch = 100, ist EB faktisch = 0. Oben aber haben wir gezeigt, daß bei EB = 0 die Leerbuchtheorie und mein Postulat die gleichen Ergebnisse erbringen – aber eben auch nur bei EB = 0.
Einwendung 5: Wenn der Abfluß aus dem Lager unregelmäßig ist, reicht eine auf EB und M beruhende Berechnung nicht aus.
Erwiderung 5: Das ist richtig, aber nicht relevant. Wir haben eine starre Entnahme und damit einen gleichmäßigen Lagerabfluß angenommen, um das Modell nicht mit unnötigen Details zu überfrachten. Es soll einfach und verständlich gehalten werden.
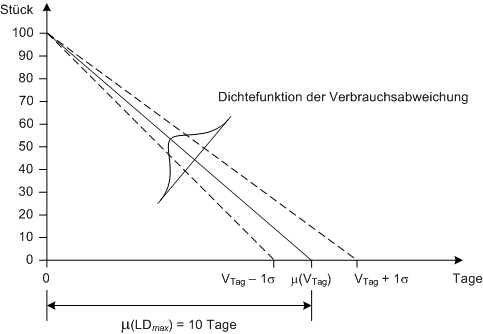Man beachte auch diese Grafik:
Schwankt der Tagesverbrauch, den wir in der Modellrechnung mit 10 Stück/Tag angenommen hatten, so kann man diese Schwankung als Standardabweichung von einem mittleren Verbrauch pro Tag beschreiben. Die Gauß'sche Normalverteilung kann verwendet werden, die Wahrscheinlichkeit einer maximalen Lagerdauer unter oder über einem bestimmten Grenzwert zu bestimmen. Unser Beispiel mit einem starren Lagerabgang von 10 Stück am Tag ist ein Sonderfall dieser allgemeineren Darstellung, weil wir ein Sigma = 0 implizit vorausgesetzt haben. Wäre Sigma > 0, so wäre nur noch eine Wahrscheinlichkeitsaussage über die maximale Lagerdauer möglich. Es gilt aber immer noch
Auch diese beiden Aussagen müßten dann mit einem Sigma versehen werden. Das würde sie aber nicht falsifizieren, sondern nur komplizierter machen. Wir haben daher die Vereinfnachung Sigma = 0 angenommen, um das Modell übersichtlich zu halten.
Da die maximale Lagerdauer also nach wie vor (bei Durchschnittsbewertung nach §240 Abs. 4 HGB oder IAS 2.25) das Doppelte der durchschnittlichen Lagerdauer beträgt, folgt:
Dies deckt sich offenbar mit den oben gewonnenen Erkenntnissen. Es bestätigt insbesondere die Konstanz der maximalen Lagerdauer unabhängig von Bestellmenge M und damit der Zahl der Bestellvorgänge. Es spielt für die maximale Lagerdauer keine Rolle, ob ich jeden Tag zehn Stück bestelle oder alle zehn Tage hundert Stück, solange mein maximal möglicher Lagerbestand bei 100 Stück bleibt. Einige fanden es schwer, das zu akzeptieren – wohl, weil die falschen Schulbuchformeln für Lagerumschlag und Lagerdauer damit widerlegt werden:
Dies ist nämlich auch in sich schon ein weiterer Beweis gegen die Lehrbuchtheorie: Da die maximale Lagerdauer nur vom Tagesverbrauch und vom Höchstbestand abhängt, können die mit der "Schulbuchformel" oben ermittelten Lagerumschlags- und Lagerdauerwerte nicht richtig sein, da sie über der maximalen Lagerdauer liegen, wenn der Eiserne Bestand größer null ist.
Einwendung 6, 7, 8, …, n: "Sie haben nichts verstanden", "Lassen Sie es, Sie können das nicht", "Sie sind ein…", "das macht doch keiner", usw. usf.
Erwiderung 6, 7, 8, …, n: Es ist erstaunlich, wie oft ich für diesen Artikel beschimpft wurde. Emotionale Äußerungen sind mir nicht unbekannt, wenn ich über politische Themen oder die Pyramidenspieler schreibe – besonders die sogenannten Network Marketer sind dafür bekannt, heftige Feedbacks auf meine gelegentlichen Artikel zu schreiben. Daß aber ein so mathematisches und theoretisches Thema so auf der Beziehungsebene ausgetragen werden soll, ist immerhin erstaunlich. Es scheint, daß ich einigen Dozenten hier ein lang gehegtes Unterrichtsthema beschädigt habe?
Ein Fazit: Alte Theorien verschwinden so langsam, weil nicht nur die Professoren, die sie verbrochen haben, sondern auch ihre Schüler sterben müssen, bevor neue Gedanken möglich sind. So scheint das auch hier zu sein: einer schreibt die falschen Formeln vom anderen ab, und keiner hinterfragt sie. Ich muß sogar gestehen, es anfangs, vor vielen Jahren, auch so gemacht zu haben. Erst als ich anfing, solche Systeme für Firmen zu programmieren bemerkte ich, daß die "offizielle" Lehre nicht stimmen kann. Ich bin gespannt wie lange es dauert, bis die hier widerlegte "Leerbuchtheorie" endlich aus den Lehrbüchern verschwindet. In meinen Büchern steht selbstverständlich mein Postulat; während zum Teil sogar Tippfehler beim Verlag gerügt wurden, hat sich hierüber aber noch keiner echauffiert. Es scheint also, daß die eingefahrenen Gleise so schwer zu verlassen sind daß man nichtmal merkt, wenn etwas Neues entsteht.
Links zum Thema: Lagerdauer und Lagerumschlagshäufigkeit: Gravierende Fehler in Lehrbüchern für Auszubildende | Lagerwesen: warum sich die Lagerdauer bei FIFO verdoppelt | Formelsammlung der BWL | Skript zur Disposition | Skript zur Bestellmengenrechnung (interne Links)
