Schon vor längerer Zeit demonstrierten wir, wie eine Break Even Rechnung ohne Mengenangabe funktioniert. Das mag zwar völlig unrealistisch sein, aber wen interessiert das im Vorfeld einer IHK-Prüfung? Jetzt geht das Gespenst eines neuen Prüfungshammers um in den Lernzirkeln der Nation, die exakte (also nicht näherungsweise) interne Zinsfußrechnung ohne Computer. Was Generationen von Dozenten als unmöglich bezeichneten, soll der verdutzte Prüfling plötzlich unter Zeitdruck und Notenstreß zuwege bringen. Wir zeigen, wie es geht – zur Freude der Prüfungslyriker! 😉
|
Der Fall: Zur Finanzierung einer Anlage im Anschaffungswert von 50.000 € plant ein Unternehmen eine Kreditaufnahme. Insbesondere wird eine Finanzierungsform gesucht, die zu Anfang tilgungsfrei ist, weil zunächst ein neues Produkt am Markt eingeführt werden soll. Ihre Hausbank schlägt vor, den Kredit als Fälligkeitsdarlehen auszugestalten. Insbesondere sollen 5 Jahre nach 100%iger Auszahlung der Kreditsumme der Kredit und die Summe aller Zinsen durch eine einzige Zahlung i.H.v. 75.000 € getilgt werden. |
Das sieht soweit unauffällig aus und scheint eine mehr oder weniger brauchbare Aufgabe über Zinsrechnung oder Finanzierung zu werden. Der Adrenalinspiegel des Prüfungsteilnehmers steigt aber deutlich bei der Lektüre der Aufgaben. Wie so oft geht es mit einer vergleichsweise einfachen Aufgabe los:
|
Aufgabe 1: Sie könnten sich anderweitig einen Kredit gleicher Höhe zum Zins von effektiv 10% beschaffen. Ist das Angebot Ihrer Hausbank gegenüber dem anderweitigen Angebot vorteilhaft? |
Hier ist der Barwert der beiden Zahlungsvorgänge mit einem Kalkulationszins von 10% zu rechnen:
| t | Zahlung | Barwert |
| 0 | – 50.000,00 € | – 50.000,00 € |
| 5 | 75.000,00 € | 46.569,10 € |
| Summe | + 25.000,00 € | -3.430,90 € |
Das Fremdangebot ist also offensichtlich nicht vorteilhaft: es hat eine Verzinsung die höher liegt als die der Hausbank. Das ist soweit recht unproblematisch; lernpsychologisch könnte sich vielleicht nur als hinderlich erweisen, daß lediglich der Auszahlungszeitpounkt (t=0) und der einzige Rückzahlungszeitpunkt (t=5) ohne dazwischenliegende Perioden zu berücksichtigen sind. Das behindert alle, die die interne Zinsfußmethode schematisch gelernt und nicht wirklich verstanden haben, ist aber nur eine kleine Hürde im Vergleich zur jetzt kommenden Knallschote:
|
Aufgabe 2: Wie hoch ist die Effektivverzinsung des Angebotes der Hausbank? Ermitteln Sie den Effektivzins unter der Annahme, daß keine weiteren Faktoren zu berücksichtigen sind. Verwenden Sie eine Methode, die ein präzises Ergebnis vermittelt, also keines der Näherungsverfahren. |
Au weia! Und da haben wir doch seit Generationen von Dozenten gesagt bekommen, daß dies gar nicht ginge, oder, seit Erfindung so nützlicher Excel-Funktionen wie der Zielwertsuche, nur per Computer, also nicht in Prüfungen. Und die fleißigen unter uns haben gar die Näherungsmethode per Triangulation auswendig gelernt, und jetzt dürfen wir die nicht anwenden? Eine exakte Lösung ist aber auch ohne Zielwertsuche und ohne Computer mit einfachen Mitteln ausschließlich über die Potenzfunktion des Taschenrechners möglich. Hierzu ist zunächst zu bedenken, daß beim Effektivzins der Barwert null ist. Es muß also gelten:
| t | Zahlung | Barwert |
| 0 | – 50.000,00 € | – 50.000,00 € |
| 5 | 75.000,00 € | 50.000,00 € |
| Summe | + 25.000,00 € | 0,00 € |
Wie hoch ist aber der hier zugrundegelegte Zins? Das kann man herauskriegen, indem man sich vergegenwärtigt, daß die allgemeine Kapitalwertformel
![]()
ist. Die Summen aller Zahlungssalden müssen also addiert werden. In diesem individuellen Fall (!) enthält die zu addierende Zahlungsreihe aber nur einen einzigen Rückzahlungsbetrag. Setzt man den ein, so erhält man:
![]()
Aus der allgemeinen Kapitalwertformel läßt sich kein exakter Wert berechnen, weil man nicht nach i umstellen kann, denn der Zins i steht hinter dem Summenzeichen. Hier ist das Summenzeichen aber verschwunden. Man muß also nur noch nach i umstellen und hat die präzise Lösung. Gehen wir also zunächst davon aus, daß gilt
![]()
Jetzt kann man sagen:
![]()
Also gilt:
![]()
Das heißt aber:
![]()
Daher kann man sagen:
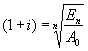 oder
oder 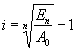
Im vorliegenden Fall bedeutet dies:
![]()
Wendet man diesen Zins auf die 75.000 € Rückzahlung an, so erhält man genau die oben skizzierte Barwerttabelle. Dividiert man die 75.000 € Rückzahlung durch 1,0884471771, so erhält man genau 50.000 €.
Hier wäre noch anzumerken, daß man mit einem Taschenrechner, der keine 5. Wurzel ziehen kann, natürlich die 5. Wurzel auch berechnen kann, in dem man eine Potenz zu einem Fünftel berechnet.
Diese Methode gilt nur für den Fall des Fälligkeitsdarlehens mit einer einzigen Rückzahlung, ist also eigentlich wenig realistisch: wo gibt es schon Fälligkeitsdarlehen ohne Zinszahlungen während der Laufzeit? Aber ist das vor einer Prüfung die richtige Frage? Zero Bonds zeigen allerdings eine dem hier angenommenen Verhalten ähnliche Zahlungsreihe und können unter Umständen auf diese Art berechnet werden; auch hier ist der praktische Nutzen der Rechenmethode jedoch gering. Aber ob das auch die Prüfungslyriker wissen?
Die Aufgabe ist geradezu ein Lehrbuchbeispiel für meine Dauerpredigt, man dürfe nicht auswendig lernen (und solle möglichst nicht mal mitschreiben), sondern müsse die den Dingen zugrundeliegenden Strukturen erkennen und verinnerlichen: wer die ihm präsentierten Standardmethoden schematisch auswendig lernt, scheitert mit Sicherheit an dieser Knallschote, denn hier ist ein unkonventioneller Lösungsweg erforderlich, der sich nur erschließt, wenn man das der Effektivzinsrechnung zugrundeliegende Verfahren wirklich verstanden hat!
Links zum Thema: Break Even Rechnung: so versuchen die Prüfungslyriker Euch zu kippen! | Totgesagte leben länger: Tageberechnungsmethoden in der Zinsrechnung (interne Links)







